نرخ بازده موزون زمانی و نرخ بازده موزون پولی

زمانیکه یک شخص یا صندوق سرمایه گذاری با وجه نقد ثابت در بازار سهام در حال سرمایه گذاری است به راحتی می تواند میزان بازده سرمایه گذاری خود را پس از پایان یک دوره محاسبه کند. برای این منظور ارزش آخر دوره سبد سرمایه گذاری منهای ارزش اول دوره می گردد و این اختلاف بر ارزش اول دوره تقسیم می شود.

اما گاهی اوقات ممکن است شخص سرمایه گذار یا صندوق سرمایه گذاری، دائما مبالغی را برداشت و یا به سرمایه گذاری اضافه کند. در این حالت، در دوره های زمانی مختلف بازده های مختلفی کسب می شود و از آنجا که مبالغ سرمایه گذاری شده دائما در حال تغییر بوده است محاسبه دقیق میزان بازدهی، پروسه نسبتا پیچیده ای دارد.

به این منظور دو روش نرخ بازده موزون زمانی و نرخ بازده موزون پولی مورد استفاده قرار می گیرد. امروزه در صنعت مالی، بازده موزون زمانی مورد قبول است و استاندرد صنعت می باشد. زیرا ارزیابی منصفانه تری نسبت به عملکرد مدیران صندوق های سرمایه گذاری ارائه می دهد.

نرخ بازده موزون پولی (MWRR)

زمانیکه صحبت از عملکرد سرمایه گذاری است بازده موزون پولی، همانند نرخ بازده داخلی(IRR) عمل می کند. نرخ هزینه سرمایه(WACC) می تواند به عنوان حداقل نرخ قابل قبول IRR مد نظر قرار گیرد تا خالص ارزش فعلی(NPV)، مثبت شود. بنابراین:

منفی WACC < IRR =  NPV

صفر WACC = IRR =  NPV

مثبت WACC > IRR =  NPV

در مدیریت سرمایه گذاری، بازده موزون پولی، نرخی است که ارزش فعلی جریانات نقد ورودی را برابر با ارزش فعلی جریانات نقد خروجی می کند. این بدان معنی است که نرخ بازده برابر با نرخ تنزیل می شود.

این روش جهت رصد عملکرد مدیران سرمایه گذاری، مناسب نیست. زیرا بازده می تواند تحت تاثیر واریز و برداشت های قابل توجه مشتریان قرار گیرد. چنین تغییراتی در اندازه سرمایه گذاری می تواند عملکرد مدیران را بطور غیر منصفانه ای خوب یا بد نشان دهد. زیرا تصمیمات مشتریان درباره واریز و برداشت، خارج از کنترل مدیران می باشد.

برای محاسبه نرخ بازده موزون پولی باید ارزش فعلی جریانات نقد ورودی مساوی با ارزش فعلی جریانات نقد خروجی قرار داده شود و سپس معادله جهت یافتن نرخ تنزیل حل گردد. محاسبه این معادله نیازمند ماشین حساب مالی یا نرم افزارهای صفحه گستره است.

بطور کلی جریانات نقد ورودی و خروجی به شرح زیر می باشند.

جریان های نقد خروجی:

1- وجوه پرداخت شده بابت سرمایه گذاری

2- سرمایه گذاری های مجدد از بابت سود نقدی سهام(همانند وجوه پرداخت شده بابت سرمایه گذاری می باشد)

3- برداشت ها(وجوه برداشت شده از پرتفوی توسط سرمایه گذار)

جریانهای نقد ورودی:

1- عواید ناشی از فروش سرمایه گذاری(وجه نقدی که از بابت فروش سهام در پرتفوی باقی می ماند)

2- سود نقدی سهام

3- وجوه تزریق شده به پرتفوی توسط سرمایه گذار

پس از اینکه جریانات نقد ورودی و خروجی مشخص گردید آنها را در فرمول زیر قرار می دهیم.

فرمول محاسبه نرخ بازده موزون پولی (MWRR):

در فرمول بالا، جریانهای نقدی خروجی با علامت منفی و جریانهای نقدی ورودی با علامت مثبت در فرمول قرار می گیرند. در واقع جریانات نقد خروجی نیر مثبت بوده اند اما از آنجا که از سمت دیگر تساوی به سمت جریانات نقد ورودی انتقال داده شده اند علامت آنها تغییر کرده است.

فرض کنید یک سهامدار با سرمایه گذاری اولیه 2 میلیون تومان وارد بازار سهام می شود. در ابتدای هر یک از سال های دوم، سوم و چهارم مبلغ 200،000 تومان و همچنین در ابتدای سال پنجم نیز مبلغ 1،000،000 تومان به سرمایه گذاری خود اضافه می کند. این سرمایه گذاری در انتهای سال پنجم دارای ارزشی به میزان 4،124،983 تومان می باشد. جدول زیر، این گردش را بطور خلاصه نشان می دهد.

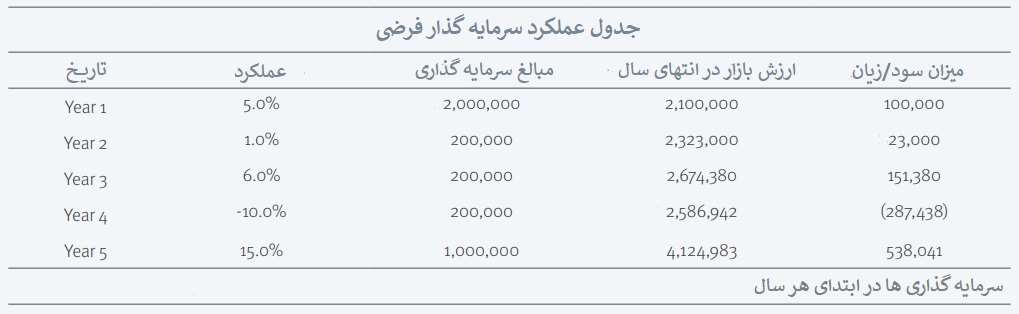
توجه داشته باشید که این جریانات نقدی از دید یک شخص سرمایه گذار می باشد. بنابراین هر بار که از وجوه نقد سرمایه گذار کسر می شود به عنوان جریان نقدی خروجی در نظر گرفته شده و با علامت منفی در فرمول قرار می گیرد.

با قرار دادن ارقام فوق در فرمول میانگین موزن بازده پولی، رقم 3.84% بدست خواهد آمد.

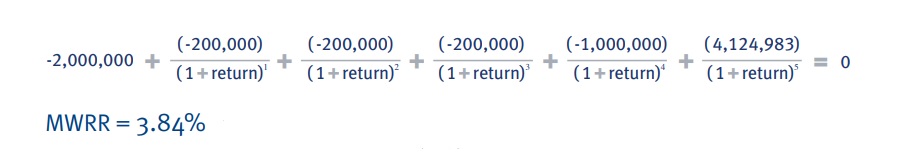
نرخ بازده موزون زمانی (TWRR)

نرخ بازده موزون زمانی، یک میانگین هندسی از عملکرد سبد سرمایه گذاری است. محاسبه بازده موزون زمانی نیازمند تقسیم دوره سرمایه گذاری به چندین دوره زمانی است. سپس عملکرد هر دوره محاسبه می گردد. جهت محاسبه نرخ بازده موزون زمانی می توان از فرمول زیر استفاده کرد.

در بالا علاوه بر فرمول بازده موزون زمانی، نرخ بازده با داده های مثال قبل نیز محاسبه شده است که عدد 3.07% بدست آمده است. در این مثال، بازه های زمانی به دوره های یکساله تقسیم شده است. زیرا واریزها و برداشت ها در ابتدای هر سال صورت گرفته است.

در این روش، بازده هر دوره، وزن یکسانی دارند. همچنین زمان و اندازه واریز و برداشت ها تاثیری بر میزان بازدهی نخواهند داشت. از آنجا که در این مثال، پنج بازه زمانی وجود دارد تاثیر هر دوره بر بازده کل 20% می باشد. در بهترین حالت می توان بازده موزون زمانی را در دوره های روزانه محاسبه کرد.