ارزش زمانی پول + فرمول ها

ارزش زمانی پول به چه معنی است؟

پول دارای ارزش زمانی است. وجه نقدی که شما امروز در دست دارید با همان میزان پول در یک سال دیگر دارای ارزش های متفاوتی هستند. معمولا پول نقد به علت وجود تورم ارزش خود را از دست می دهد. ما جهت تصمیمات مربوط به مصرف، پس انداز، قرض دادن و قرض گرفتن نیاز به محاسبه ارزش زمانی پول داریم. علت اینکه یک موسسه مالی بعد از اعطای وام به مشتری خود، پول بیشتری طلب می کند کاهش ارزش پول در طول زمان است. به این مبلغ اضافه که علاوه بر اصل سرمایه پرداخت می شود بهره می گویند. این بهره بصورت درصد سالیانه بیان می شود. بهره می تواند تفاسیر مختلفی به شرح زیر داشته باشد.

1- سود بدون ریسک: شما می توانید هر زمان که تمایل داشته باشید وجه نقد خود را در بانک سپرده و یا در اوراق با درآمد ثابت شرکت ها سرمایه گذاری کرده و به سود بدون ریسکی دست پیدا کنید.

2- هزینه فرصت: زمانیکه یک سرمایه گذار دست به سرمایه گذاری می زند این نرخ بهره بدون ریسک را از دست می دهد.

3- تورم: میزان بهره معمولا با مقدار تورم یک کشور رابطه مستقیمی دارد.

پولی که الان در دست داریم در آینده دارای ارزش دیگری است که به آن ارزش آتی گفته می شود. همچنین وجهی که در آینده قرار است دریافت یا پرداخت کنیم در زمان حال می تواند قدرت خرید متفاوتی داشته باشد که به آن ارزش فعلی گفته می شود.

ارزش آتی مبلغ ثابت

فرض کنید مبلغ 1،000،000 تومان را می خواهیم در بانک سپرده کنیم. میزان بهره 20% می باشد. بعد از یک سال چند تومان در حساب بانکی خود خواهیم داشت؟

یک میلیون بعلاوه 20 درصد از یک میلیون تومان برابر می شود با یک میلیون و دویست هزار تومان.

1،200،000 =(0.2+1) × 1،000،000

بنابراین اگر بخواهیم ارزش آتی یک مبلغ ثابت را برای یکسال دیگر محاسبه کنیم از فرمول زیر استفاده می کنیم:

در این فرمول FV ارزش آتی، PV ارزش فعلی و r نرخ بهره اعلام شده سالانه می باشد.

حال فرض کنید مبلغ یک میلیون تومان را برای دو سال سپرده شود. در این حالت در سال دوم، 20 درصد به رقم یک میلیون و دویست هزار تومان اضافه می گردد. بدین ترتیب کل وجه در پایان سال دوم  برابر است با:       1،440،000 =(0.2×1)×1،200،000

همانگونه که مشاهده شد مبلغ بهره در سال اول 200،000 تومان و در سال دوم 240،000 تومان است. چرا که علاوه بر بهره اصل سرمایه، بهره سود سرمایه نیز اضافه شده است. بنابراین بهره هر دوره بیشتر از بهره دوره قبل خواهد بود که به آن بهره مرکب گفته می شود. جهت محاسبه ارزش آتی چند دوره از فرمول بالا استفاده می کنیم. تنها کاری که باید انجام دهیم نرخ داخل پرانتز را به توان تعداد دوره ها می رسانیم.                                                   

ارزش فعلی مبلغ ثابت

حال فرض کنید مبلغی وجه نقد در آینده به ما پرداخت خواهد شد و می خواهیم ارزش فعلی آن را محاسبه کنیم. با این محاسبه می توانیم تشخیص دهیم که قدرت خرید میزان مبلغی که در آینده بدست می آوریم برابر با قدرت خرید چه مقدار وجه نقد در زمان حال است. برای محاسبه ارزش فعلی مبلغ مشخصی در آینده، از فرمول زیر استفاده می کنیم.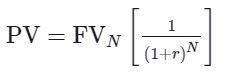         

اگر از اعداد مثال بالا استفاده کنیم FV برابر با 1،440،000 تومان، r برابر 20% و N برابر 2 سال می باشد. با جایگذاری اعداد در فرمول ارزش فعلی، رقم یک میلیون تومان بدست می آید.

ارزش آتی اقساط مساوی

گاهی اوقات مبلغ ثابتی در چند دوره پرداخت می شود و پس از چندین دوره مبلغی یکجا به سرمایه گذار باز پرداخت می گردد. نمونه این نوع پرداخت، برخی از بیمه های عمر و سرمایه گذاری می باشد. در این حالت برای اینکه بدانیم ارزش آتی مجموع پرداخت هایی که در زمان های مختلف پرداخت شده اند چقدر می باشد از فرمول ارزش آتی اقساط مساوی استفاده می کنیم. این فرمول به شکل زیر می باشد.

در این فرمول، A مبلغ هر قسط می باشد.

ارزش فعلی اقساط مساوی

بر خلاف ارزش آتی اقساط مساوی که ارزش اقساط مساوی در آینده را محاسبه می کند، فرمول ارزش فعلی اقساط مساوی مشخص می کند که مجموع پرداخت هایی ثابت در پایان چند دوره برابر با چه مبلغی در امروز می باشد. فرمول ارزش فعلی اقساط مساوی به شرح زیر است.

بیشترین استفاده از فرمول ارزش فعلی اقساط مساوی جهت محاسبه مبلغ هر قسط وام می باشد.

فرض کنید شما یک وام 50 میلیون تومانی 3 ساله با باز پرداخت فصلی دریافت کرده اید. نرخ بهره سالانه این وام برابر با 20% می باشد. حال می خواهید مبلغ هر قسط را محاسبه کنید.

در اینجا PV، مجموع ارزش فعلی اقساط مساوی است که برابر با 50 میلیون تومان می باشد. تعداد اقساط باز پرداخت وام با N نمایش داده می شود. اقساط این وام، 3 ساله و در هر سال 4 بار پرداخت می شود. بنابراین N برابر با 12 ( 3 ضربدر 4) است. حرف لاتین r، بهره هر دوره را نشان می دهد. بهره سالیانه 20% تقسیم بر 4 شده و بدین ترتیب، بهره هر دوره پرداخت برابر با 5% می باشد.

حال با جایگزینی اعداد و مجهول قرار دادن A، مبلغ هر قسط برابر با 5،641،000 تومان خواهد بود.

نرخ بهره موثر سالانه

اگر در مثال های بالا درصد بصورت سالانه اعلام شود اما پرداخت ها بصورت میاندوره ای باشد متغیر N ضربدر تعداد دوره ها و متغیر r تقسیم بر تعداد دوره های پرداخت می شود. فرض کنید N دوساله و r برابر 20% باشد. اما پرداخت ها بصورت سه ماهه انجام شود. بنابراین در یک سال چهار بار پرداختی خواهیم داشت. در این حالت دوره های پرداخت (N) برابر 8=4×2 و میزان بهره (r) برابر با 5%=20/4 خواهد بود. هر چه تعداد دوره های پرداخت بیشتر می شود درصد بهره سالیانه بالاتر خواهد بود که به آن نرخ بهره موثر سالانه گفته می شود. نرخ بهره موثر سالانه از فرمول زیر قابل محاسبه است.

                                 تعداد دوره های پرداخت در سال ^(نرخ بهره در هر میان دوره +1 ) = نرخ بهره موثر سالانه

بیشترین بهره زمانی به سرمایه گذار پرداخت می شود که محاسبه بصورت روز شمار باشد. گرچه ممکن اجازه برداشت سود بهره، روزانه نباشد.

ارزش فعلی پرداخت مادام العمر

همچنین ارزش فعلی یک پرداختی مادام العمر برابر است با:     PV= A/r    در این فرمول A مبلغ هر قسط می باشد

از این فرمول می توان برای محاسبه ارزش باز خرید مستمری بازنشستگی و برخی سهام ممتاز با سود ثابت استفاده کرد.

ارزش زمانی پول یکی از پیچیده ترین مباحث مالی است که به وفور در تصمیم گیری های اقتصادی از آن استفاده می شود. در اینجا تنها مباحث پایه ای مربوط به این موضوع مطرح شد تا بتوانید در تصمیمات مالی خود، ارزش زمانی پول را در نظر گرفته و از منابع خود بهینه تر استفاده کنید.